Calculus Lab: 5/03/2022
Integral calculus foundations
Objective: Learn to work with some key concepts and notation that comprise the foundation of integral calculus. We will approach this via the following 3 tasks- Practice using indexing notation.
- Learn to approximate the area under the graph of a function.
- Compute the exact area using limits.
I. Indexing notation
Follow
this link
and carry out the tasks described in the worksheet.
II. Approximation of areas
Next, let us learn/practice how to approximate the area under
the graph of a continuous
function \(f(x)\) on the interval \([a,b]\).
If necessary, review pages 1-4 of the following supplement.
(I) Find the approximate area under the graph of
\( f(x) = -x^3 + 8x +4 \)
between \(x=-1\) and
\(x=3\), using 8 rectangles with:
(i) left end points,
(ii) right end points, and
(iii) mid-points.
I want to see clear and detailed steps here. A simple way to do
this is to make a table with columns (or rows) showing the
values of: \(i\), \(x_i\)
and \(f(x_i)\).
Write a paragraph discussing how the left sum
and right sum are related to each other: Did you
notice any common terms in their computation? Which
of the 3 approximations is likely to be the best? Why?
Verify your answers using the Sage script below.
It will automatically calculate all 3 types of
Riemann sums if you give it your function, together with
the endpoints (\(a\) and \(b\)) and the number of
rectangles you want (\(n\)).
NOTE: Be sure to scroll down to the right place
for enetering your function information. Do not mess
with the first 15 lines of the script. User input starts
after line 22.
(II) We will now develop a general formula for finding the area in the above problem using \(n\) rectangles. The sketch below shows our \(x\)-axis and illustrates the base on which the \(n\) rectangles will sit. Each dot represents the corner of a rectangle, and the segment between dots represents the base of the rectangle.
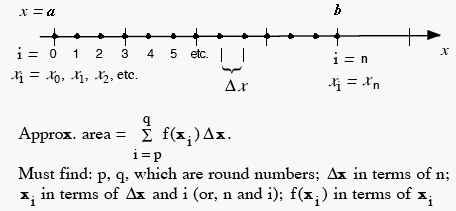
Here are the step-by-step tasks involved
(see Example 3(a) on pg. 348 of your textbook for
a clear exposition of very similar steps):
(i) Find a formula
for \(\Delta x\) that would hold for any n.
(ii) Find a formula
for \(x_i\) that only requires plugging in
n and i to
get the correct \(x\)-value.
(iii) Find a formula
for the area of the ith rectangle.
(iv) Find a formula
for the left- and right- Riemann sums. Your formula
should consist of a summation with no unknowns
in it except n. See, for example, the formula
shown in Exercise 20, pg. 342, of your textbook. (You may
leave out the limit shown in that example.)
Here
is an online summation calculator that can be used
to verify whether your formula gives you the same
answers you got in (I) above when the
number of rectangles is 8.
III. Evaluating the exact area under a curve
Suppose \(f(x) = 1 + x\), with \(a=-2\) and \(b=2\).
One (cumbersome!) way to find the exact area under
\(f\) on the interval \([-2, 2]\) is by setting up
a Riemann sum with \(n\) rectangles, and then taking
the limit as \(n \rightarrow \infty\).
Find the exact area using this method.
Here are the steps:
* Setup a right (or left) Riemann sum using n rectangles.
* Convert the sum to a simple formula that
involves only n.
* Find the limit as n goes to infinity. That is your answer.
See pg. 346 of textbook for relevant formulas.