Calculus Lab: 3/29/2022

A seriously silly model of romantic love!
How do I love thee? Let me model the ways!
- My apologies to Elizabeth Barrett Browning for nerdifying her lovely poem!

(Adapted from various sources. But if you're seriously interested, check out this article!)

Prelude: Please complete this brief self-assessment of your romantic personality before working on the rest of today's lab.

The scene: Juliet loves Romeo, and Romeo loves Juliet, at least at time \(t=0\). The question is, how will their feelings evolve with time, and as they meet other, potentially fascinating, new people! Here is our modeling strategy:

  • We will model the rate of change in their feelings, with respect to time.
  • Let \(J(t) =\) a function that represents Juliet's love for Romeo at time \(t\). The sign and magnitude of \(J(t)\) indicate how much Juliet loves (or hates, if it is negative) Romeo.
  • Let \(R(t) =\) a similar function of Romeo's feelings about Juliet.
Love is an ever changing function

To help you get comfortable with these love functions and their phase plots, let us begin with a warmup exercise.

Each graph below shows the time history of various hypothetical love affairs between Juliet and Romeo. Write a few sentences discussing what is happening in each graph.

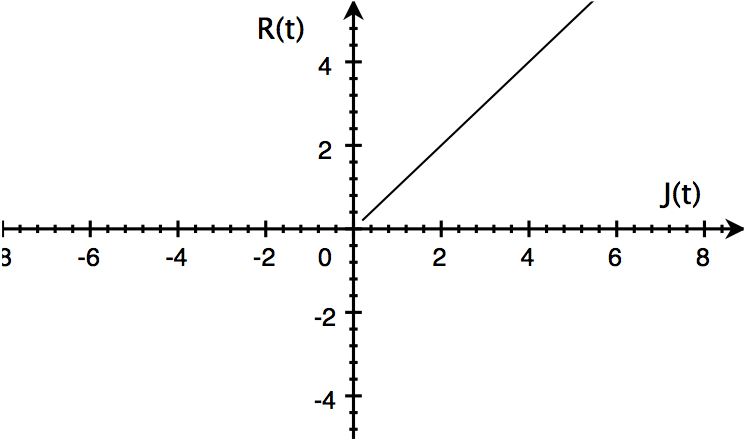Fig. 1

Fig. 2

Fig. 3

Fig. 4

Building a simple love-affair model
For simplicity, we will assume that there are only two variables that affect Juliet's future feelings for Romeo: (i) her own current feelings about him, and (ii) his current feelings towards her. And similarly, there are only two variables that affect Romeo's future feelings about Juliet.

As usual, we want to think in terms of the derivatives \(\displaystyle J^\prime(t)\) and \(\displaystyle R^\prime(t)\), in order to model \(J(t)\) and \(R(t)\). Here are some question to explore:

  • Suppose we ignore the magnitudes of \(J(t)\) and \(R(t)\), and consider only their signs. Write a couple of sentences discussing how many different combinations of feelings are possible, and what they are (e.g., love-hate, love-love, etc.).
  • We want to express \(J^\prime\) and \(R^\prime\) as functions of the variables they depend upon. To help you think through this, here are some possible scenarios where you can apply your understanding of the sign of derivatives to predict where Juliet's love is heading: (i) \(J^\prime = 0.3 \; J\)   [remember compound interest on bank accounts?];
    (ii) \(J^\prime = 0.3\; R\) ;   (iii) \(J^\prime = -0.3\; J\) ;   (iv) \(J^\prime = -0.3\; R\)

    In practice, we want \(J^\prime\) to depend on both \(J\) and \(R\) (since we assumed her future feelings depend on both \(J\) and \(R\)). Here is an example of this situation: Suppose Romeo is primarily connected to his own feelings and disconnected from Juliet's. And suppose Juliet has the opposite personality. Then, one simple model for \(J^\prime\) and \(R^\prime\) would look like:
          \(J^\prime = - J + R \)
          \(R\;^\prime = - J + R \)

    Here the negative signs on the 1st term suggest both lovers respond negatively when Juliet's love for Romeo increases! The positive signs on the 2nd term suggests both lovers fall deeper in love as Romeo's love for Juliet increases. True, it's weird, but there's plenty of weirdness in the real world, isn't there!

    Construct a few other simple models of this type. That is:
        \(J^\prime = \) term(s) that  depend on \(J\) and \(R\)
                      Explain what sign you want for the term(s) and why?
        \(R^\prime = \) term(s) that depend on \(J\) and \(R\)
                      Explain what sign you want for the term(s) and why?

A general formulation of the model that includes all the cases considered above is
                      \(J^\prime = a J + b R \)
                      \(R^\prime = c J + d R \)

where all the coefficients denote constant parameter values that model different personality types and/or behavior traits. For example, here is one classification scheme based on Romeo's personality that has been proposed in the literature:

  1. Eager beaver: \( c > 0\) and \( d > 0\) (Romeo is encouraged by his own feelings as well as by Juliet's.)
  2. Narcissistic nerd: \( c < 0\) and \( d > 0\) (Romeo wants more of what he feels, but retreats from Juliet's feelings.)
  3. Cautious lover: \( c > 0\) and \( d < 0\) (Romeo retreats from his own feelings, but is encouraged by Juliet's.)
  4. Hermit: \( c < 0\) and \( d < 0\) (Romeo retreats from his own feelings as well as from Juliet's.)
Explore the model's predictions
The four parameters \(a\), \(b\), \(c\), \(d\), in the general formulation above can be chosen to mimic different personality types. For example, an affair between two Eager beavers would correspond to positive values for all 4 parameters.

Pick a few different personality combinations and explore what the model predicts about their love affair. Choose any convenient values for the parameters in the range of the behavior types you want. (E.g., values like 1 and \(-1\) are simple and perfectly reasonable to use.) For each case, interpret your results and predict the evolution of Romeo and Juliet's feelings for each other in the long-term. Be sure to try different starting points for each situation; e.g., \(J(0)\) , \(R(0)\) need not always be positive.

Use Apple Grapher or the Sagecell script below to carry out your explorations.

 

A contrived love affair

It is not too hard to design a model to mimic any long-term behavior we want. For example, suppose we want both lovers to stay in love permanently, after an initial period of meandering and uncertainty! Consider the following model:
                      \(J^\prime = -0.2(J-3) - (R-4) \)
                      \(R^\prime = (J-3) - 0.2(R-4) \)

Pick any choice of initial values for \(J\) and \(R\) -- in fact, try various combinations such as hate-hate, love-hate, etc. Use the Grapher (here is a screenshot showing an example) or Sage (script below) to run these simulations and discuss your results: what are the values of \(J(t)\) and \(R(t)\) in the long-term? Arguing from a calculus perspective, can you conjecture why? What are the personality types of Romeo and Juliet in this model (e.g., Eager beaver, Narcissistic nerd, etc.)? Can you think of a simple change to the model that would make them both hate each other in the long-term?

 

More complex love affairs (optional)

Try at least one of these, just for fun! No need to include in your lab report.

As you might suspect, things get much more interesting when we try to model non-linear personalities, or other more complicated situations such as 3-way affairs or polyamorous relationships.

  1. Nonlinear personalities

    Here is one simple way to make the Juliet-Romeo model nonlinear

                          \(J' = a J + b R(1-|R|) \)
                          \(R' = c J(1-|J|) + d R \)

    Can you conjecture what type of real-life behavior the nonlinear terms might capture (assume \(b\) and \(c\) are positive)? Depending on the choice of parameters, different solution behaviors can be seen. For example, try to run some simulations in the Grapher (see example screenshot) or Sage (see script below) with \(a=b=-2\) and \(c=d=1\). To really understand what is going on, you will need to try a few different initial values for \(J(0)\) and \(R(0)\).

     

  2. A 3-way affair
    Suppose Juliet has an affair with someone (say, Sky). A model will be much easier to develop if she keeps the affair a secret from Romeo! In that case there will be 2 equations for Juliet, plus 1 each for Romeo and Sky. Here is one example of such a model

                          \(J_R^\prime = a J_R + b (R-S) \)
                          \(J_S^\prime = a J_S + b (S-R) \)
                          \(R^\prime = c J_R + d R \)
                          \(S^\prime = e J_S + f S \)

    where \(J_R(t)\) and \(J_S(t)\) are functions that represent Juliet's love for Romeo and Sky, respectively. As before, \(R(t)\) and \(S(t)\) represent the respective partners' love for Juliet. If you assume positive parameter values for \(a\)-\(f\), can you conjecture meaningful interpretations for all the terms in this model?

    Despite the seeming complexity of this last model, it is still linear, and has a fairly limited range of solution behaviors. To see chaotic solution behaviors it is necessary to include nonlinear terms in the model.

 

Disclaimer: Do not use these models to predict anything in your own (or in your friends') real-life romantic situations!