Calculus Lab: 4/19/2022

(I) Newton method: Exposition
Background
One of the more creative and practically useful applications of linear approximation is the Newton method, which has been widely used in many disciplines for decades. The goal of Newton's method is to find the roots of general nonlinear equations of the form \(f(x)=0\).

Broadly, the strategy consists of these steps:

  • Pick some initial guess for the root, say, \(x=a\).
  • Find the tangent line approximation of \(f(x)\) at \(x=a\).
  • Find the \(x\)-intercept of that tangent line. Suppose we call it \(x=b\).
Then \(x=b\) is an approximation to the root of \(f(x)=0\).   In other words, \(f(b) \approx 0\).
Do you see why?

But..., it is likely a very poor approximation!
(Unless, by sheer luck, the tangent line at \(x=a\) happens to be a great approximation for \(f(x)\) on \(a < x < b\).)

This is where the genius of Newton's method comes in: You simply repeat the above steps, with a new tangent line to \(f(x)\) at \(x=b\).

Visual example
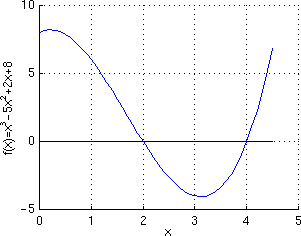
Suppose we want to find the roots of the equation \(x^3 = 5 x^2 - 2 x - 8\).
We first rewrite it as a function: \(f(x) = x^3 - 5 x^2 + 2 x + 8\).
The figure below shows the plot of this function.


The following sequence of sketches illustrates two complete iterations using the Newton method starting from the initial guess \(x_0=0.8\).


(1) Find the value of \(f(x_0)\). In this example, \(f(0.8) = 6.912\).
(2) Find tangent line at \(f(x_0)\) and extend it to intersect the \(x\)-axis at, say, \(x_1\). In the present example, \(x_1 = 2.4941\).

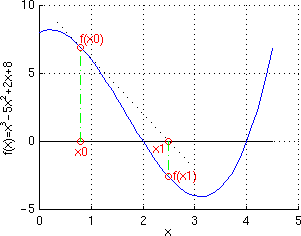(3) \(x_1\) becomes the starting point for the next iteration. In this example, \(f(2.4941) = -2.6\).
(4) Find the tangent line at \(f(x_1)\). Extend it to intersect the \(x\)-axis at, say, \(x_2\). In this example, \(x_2= 1.8866\).
Notice that each successive iteration is getting us closer to the correct root at \(x=2\).



Tasks for this part of the lab
Carry out three iterations of Newton's method to find the root of each of the following equations, starting from the indicated initial guess:

  1. \(x^4 = 1+x\).   Initial guess: \(x=0\).
  2. Same as previous equation, but initial guess is \(x=2\).
  3. \(x^3 -x = 1\).   Initial guess: \(x=1\).
  4. Same as previous equation, but initial guess is \(x=0.5\).
Comment on what your findings from doing the above problems reveal. You may find it useful to graph your functions and "see" their roots visually. Here are some queries to consider:
  • Is the initial guess important?
  • Is it possible to find all roots in cases when equations have multiple roots?
  • Are there situations where the Newton method fails? How/why?
  • How many iterations are typically needed to get a good approximation?

 

Just FYI
Here are some websites with useful/interesting graphical resources to explore the Newton method

            Desmos Newton method visuals

            A nice interactive visual for one specific example

 

(II) Related rates practice
Work out complete solutions to these exercises on pages 260-262 of your textbook:

        15, 20, 34, 38.